

"Boar" is the name of a proof of concept raytracer. Here is an introduction to the idea of exploring quadrics as fundamental rendering primitive in realtime raytracing. The name is a ploy on the usual recursive acronyms that are fashionable in the open source scene. But if I had called it "Oar" then the acronym would not neatly translate as "Eber: Bloß Ein Raytracer" in German ... :-)
Boar is not currently a usable application. Boar is not yet an open source project, either. Your eyes would bleed if you saw the source. I will make fragments of code available here, to explain and document key algorithms and formulas. Here is a summary of basic design decisions of boar.
Now for the promised code snippets that might be helpful in case you want to do your own experimenting. First there is spatial subdivision for general quadrics. Then you might need spatial subdivision with constructive solid geometry. Based on these two, Boar builds fairly nice kD-Trees:

This is just a toy scene for testing, consisting of 97 quadrics (not all of which are visible). The kD-Tree is not perfect, but does a good job separating objects from one another, and tracking their contours. One can judge this better in animation.
The tree building code uses the most basic surface area heuristic and just counts quadric primitives on either side of a potential splitting plane. A fairly large number of candidate splits are tested for each axis. The best of those attempts is then performed, and the two children are recursively subdivided further. This is a very slow method, obviously, but substantial improvements are quite possible ... watch this space. :-)
Anyway, Boar is far from realtime. The frames of the above animation took around 0.75 seconds to render on average, and that on six cores of a 3.3GHz "Westmere" Xeon. Some rendering statistics:
- average 7.7 rays per pixel (reflection, shadows, anti-aliasing)
- the average ray traverses 34 branch and 4 leaf voxels
- an average leaf contains 1.8 quadrics and 0.2 CSG intersections (i.e.
boundary between two quadrics)
- so 8 quadrics were tested per ray
Overall, an average ray took between 1900 and 2200 clock cycles. Not great, but respectable for a starting point. Multithreading is the only "hardware specific" tuning so far; and the kD-Tree the only "realtime specific" optimization.
...
From here on down, information is in reverse chronological order, blog style.
...
Partial Release 1: "Pile of Spaghetti"
Today, 23-dec-2014, I am releasing part of my code base under GPLv3. Grab the tarball if you are interested. The code is barely functional; it compiles but doesn't currently have a render loop - all platform specific, or unfinished, or "too interesting" parts have been ripped out.
Most of the code is boring and/or ugly. The one interesting bit might be in file "quadric.c++": formulas to conveniently initialize and transform quadrics in world space. I have never seen those documented anywhere else.
This release serves mainly a bureaucratic purpose. It documents a state of code, and states licensing terms. I am going to share my toy project with other parties, but I don't want to be barred from playing with it later.
Update (27-dec-2014): To my surprise, I got feedback of people who wanted to play with this. So here is a supplementary tarball with documentation of the scene description language, and an example scene file. No guarantees that the three syntaxes (in the parser, in the docs, and in the scene file) agree 100 percent with each other, but they should be close enough to get you started.
Remember that you still need a render loop that obtains rays with camera.makeRay(), finds a color through TraceRay(), and plots those pixels or writes them to an image file.
...
...
Experimenting a bit with smooth height fields based on the Zwart-Powell basis function:

This image comes from a new renderer that no longer supports constructive solid geometry. The rendering primitive I settled on is a quadric surface trimmed by basically a truncated tetrahedron. This is stored as a slab (i.e. two parallel planes) as floor and ceiling, and three more planes as side walls (which are not allowed to be parallel to each other or to the slab).
I decided to use this more complex polyhedral cage because it enables to represent triangular prisms as well as tetrahedra, and requires only a single additional coefficient for storage (17 instead of 16 for four plane equations). The prism is interesting for at least two important special cases (height fields and shapes with rotational symmetry). Without the ability to represent a prism directly, it would have to be dissected into three tetrahedra. So for now the boundaries of a quadric patch can be thought of as a "thick triangle". The ability to truncate a tetrahedron is also handy for limiting the size of long and thin bounding tetrahedra.
The hexagonal basis function I found earlier could be used for height fields as well, but it leads to a substantially larger number of patches per control point (twelve per hexagon instead of four per square). It will be useful for spherical height fields, though, which cannot be based on the cartesian grid that is home to the Zwart-Powell spline (a mix of hexagonal basis functions and simplex splines can cover a subdivided icosahedron).
...
The theory behind simplex and box splines and the like is beautiful and powerful. The concept really is simple geometry, but happening in high dimensional spaces, so it defeats human imagination and intuition (it certainly exceeds my own abilities). Nevertheless, I finally understood that bivariate basis functions, like the Zwart-Powell element, or my hexagonal basis, are not strictly limited to two-dimensional surface editing:

The basic idea is the same as Metaballs. In this example, there would be one ellipsoid component in the center, and a cylindrical component subtracted from it (which effectively drills a hole). The ears are smaller ellipsoid components added to the central blob. The shape can be grasped better in animation.
The tangent continuity of the aforementioned spline bases carries over to three dimensional "blob" components. And that ultimately implies tangent continuity of any isosurface, an example of which you can see above.
As a user interface, I think Metaballs are not a preferred choice of graphics artists. But this construction proves by demonstration that smooth quadric spline surfaces of arbitrary topology do exist and can be edited directly. Another important consequence of the above construction is that it settles the issue of what a quadric patch primitive should be: a quadric patch is a general quadric surface confined to an arbitrary tetrahedron. That is the single primitive a renderer needs to handle.
Now the big question is: can we find a better user interface for modeling these surfaces?
...
Been reading up on subdivision surfaces and box splines. Eventually I came across simplex splines (which are shadows of high dimensional tetrahedra, just like box splines are shadows of hypercubes), and the slightly exotic sqrt(3) subdivision scheme.
I noticed a funny coincidence: 1. sqrt(3) subdivision generalizes a spline basis function that was unknown beforehand (all other subdivision schemes can be traced back to a spline basis belonging to a known family), and 2. there is a gap between simplex splines and box splines: between the tetrahedron and the cube, there is another regular polyhedron, namely the octahedron.
And guess what, at least one shadow of a four dimensional octahedron does look suspiciously like a spline basis function:

This one is made of quadric pieces (unlike the sqrt(3) basis), like all the surfaces that I am interested in, and it lives on a slightly exotic hexagonal grid (like the sqrt(3) subdivision spline basis).
It is weird, but it does seem as if no one has described this family of splines yet. Until prior art is unearthed, I am taking the freedom to christen this new sibling of simplex splines and box splines Orthoplex Splines, based on the name for octahedra of arbitrary dimensionality.
...
This has almost nothing to do with boar: jugCLer. Almost.
...
Based on midedge subdivision of a toroidal control polyhedron with six by six vertices (i.e. a rough torus with hexagonal cross sections for both ring and tube), a total of 144 (= 6 * 6 * 4) quadric patches were fitted together:

Not a particular pretty torus, but tangible evidence that this works well enough to actually render an image. :-) Or an animation.
...
The individual pieces of a mid-edge subdivision surface are not quadrics (as far as I can tell, they are second order Bezier triangles). But it seems as if quadric patches can fake it quite well:
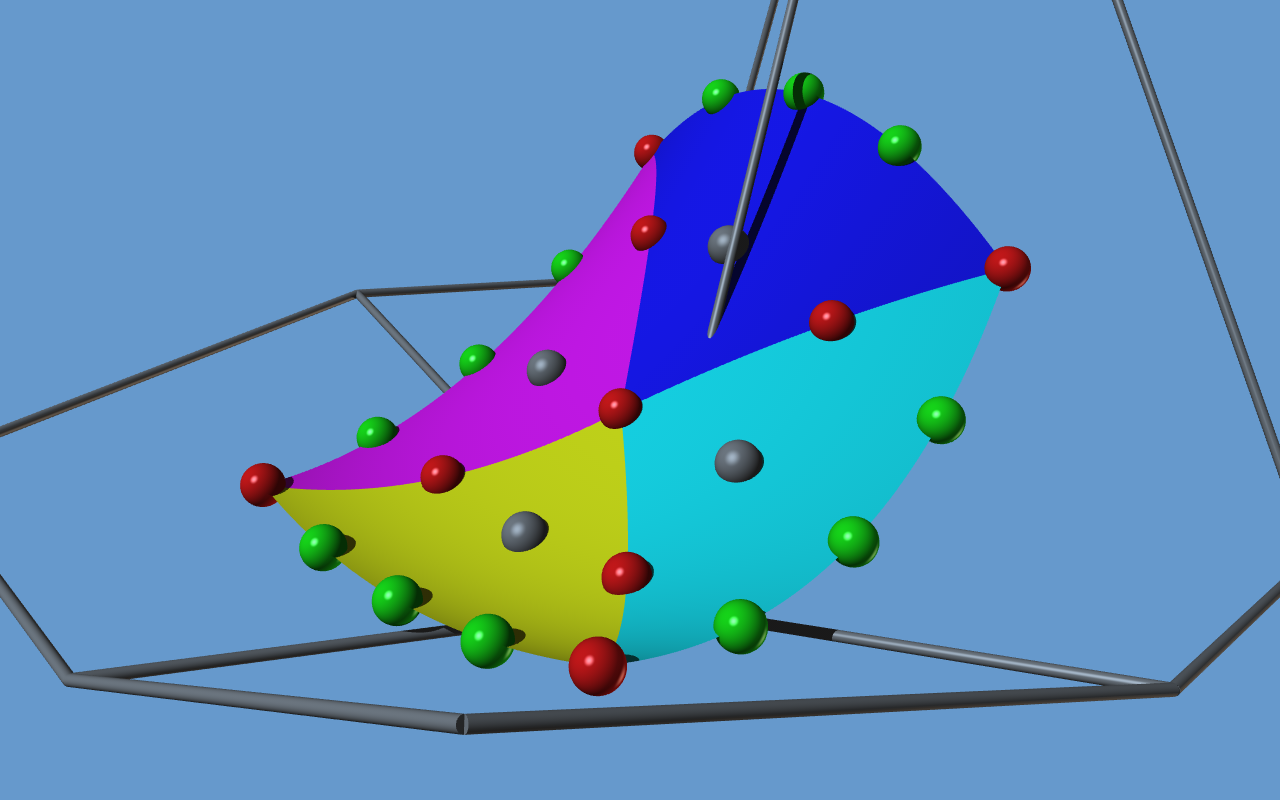
This is only a first experiment based on numerical optimization. I expect the math behind this to be rather tricky ...
...
I found out about box splines. One of them, the so-called Zwart-Powell element, can be reproduced exactly with quadric patches. It is tangent continuous everywhere, and can be decomposed Multiresolution style. This could be interesting for smooth height fields with seamless level of detail.

Addendum: there is existing research on subdivision surfaces that are based on the ZP-element. Other researchers rediscovered the same with a more thorough derivation. They claim that the limit surface has piecewise quadratic parameterization, which bodes well for good approximation with quadrics.
This is beginning to look rather promising.
...
Experimenting a bit with surfaces of revolution. Less than 300 quadric surface pieces (and a similar number of invisible separators) are required for fairly complex objects like this example. I started with an arbitrary, but smooth, generating function. This function was approximated with the square root of an ordinary second order spline (to an error bound of ±0.0005). The coefficients of the spline pieces can then be plugged directly into quadrics, yielding pieces of revolved surface.
No idea if this is of practical relevance. But at least I can generate some nice test objects now, that tax the renderer with a larger number of primitives.
...
Nothing really new, just a gallery with a few sculpting experiments.
...
Implemented inverse mailboxing, albeit as a simple direct mapped cache. No hashing; the cache is just an array of eight entries associated with a ray. Only quadric primitives are held in the cache; CSG composites benefit indirectly by having their children stored in the cache.
This reduced the number of quadric tests down to 47% of before. Net speed gain was only 10%, because kD-Tree traversal massively dominates runtime. The percentage of traversal increased from over 50% of runtime to over 65% of runtime with this optimization.
This was done in preparation of an interesting improvement to the surface area heuristic. This might have more effect on quadrics than on triangles, because a typical quadric tends to overlap more voxels than a typical triangle. But this is only guesswork, because there exist no "typical" scenes built from quadrics.
Along a similar note, this optimization for shadow rays might be a natural fit, given that Boar is a solid modeler.
...
Lost roughly 10% of speed by switching compilers from clang 3.0 to 3.1. Slightly disappointing, but fairly irrelevant at this early stage.
...
