Ever since Benoit Mandelbrot recognized and explained the fractal geometry of nature, there have been attempts to generalize the most famous fractal object, the two dimensional Mandelbrot set, to three dimensions.
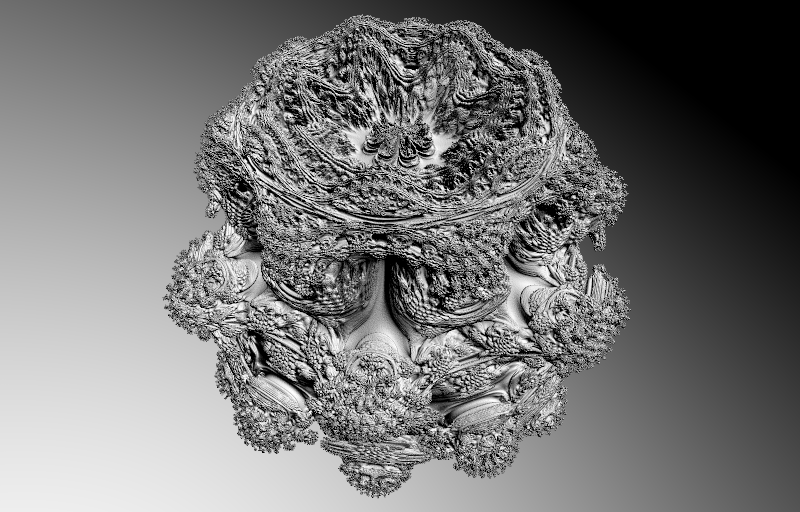
It is theoretically impossible to directly lift the underlying formula from two to three dimensions. Nevertheless, there has been some success finding visually interesting fractals in three dimensions, by abandoning some of the stricter mathematical foundations. The construction was based on spherical coordinates in order to retain certain "wrap-around" properties of the original flat Mandelbrot set. With the familiar coordinates of latitude and longitude, which we use for describing locations on earth, the resulting object is the Mandelbulb:

The Mandelbulb drew my attention, and I joined other fractal enthusiasts over on Fractal Forums on their quest for the "Holy Grail", i.e. the search for a true three dimensional Mandelbrot set. We still don't know what this ought to mean in terms of mathematical qualities, but we're having fun exploring this new style of shape-generating algorithms.
One interesting contribution that I could add was a "new" unusual and somewhat exotic coordinate system on a sphere. I call it the monopolar coordinates. Have a look at an animation of red and green grid lines on a blue sphere. The grid lines intersect at 90 degree angles; red and green are interchangeable; and there is indeed only a single pole on the sphere. (What we'd really need for the holy grail was spherical coordinates without any poles - but those are mathematically impossible).
Fairly soon it became clear that my discovery wasn't so new. Influential mathematician Bernhard Riemann had constructed essentially the same coordinate system centuries earlier. It is known as Riemann Sphere:

The monopolar coordinates can be used to replace the bipolar coordinates in the Mandelbulb computation. This results in a new fractal shape which is similar to the Mandelbulb near its single pole, but refreshingly different on the other hemisphere. Take a look at the resulting shape, slowly rotating to show all sides.
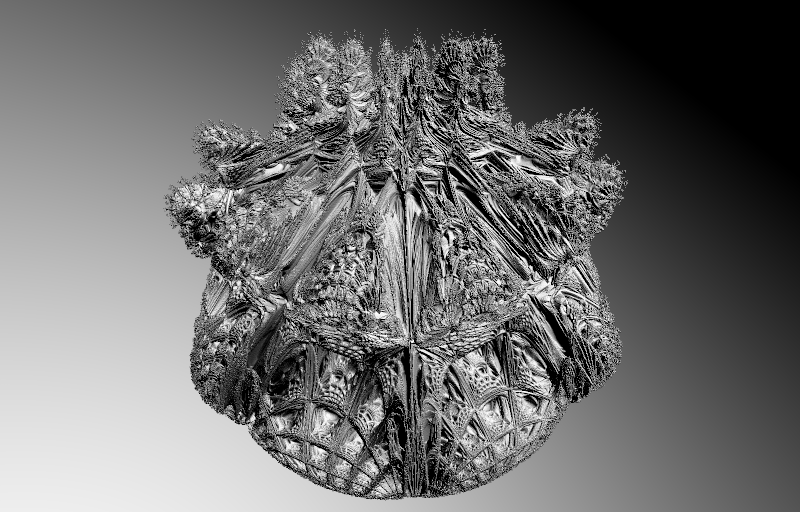
I took the freedom to christen the object "Riemandelettuce" to honour the pioneers of the underlying math, and to describe the overall shape. Here is another animation, this time a low altitude flyover.
The monopolar coordinate system can be used with shifted origin, i.e. with a translation applied to all coordinates. This doesn't make much of a difference with the usual bipolar coordinates, so it doesn't significantly alter the shape of a Mandelbulb. But the Riemandelettuce responds quite strongly to an animation of the coordinate origin, as you can see here.
All imagery of the Riemandelettuce here has been produced with an algorithm first proposed by fellow FractalForums poster Syntopia. He describes it in some detail in his blog. I made two statistical modifications to the method which speed it up by a factor around eight. The improvements are explained in replies #100 and #108 in this thread over on FractalForums.
One final bit of eye candy, in slow motion, so that the viewer has a chance to visually parse what is going on:
slomorbit01.mkv (90 seconds, ~120MB)
Minor Update: I improved the lighting a bit, and spent an undue amount of computer time on a high resolution beauty shot. After 16 days of computation time on ten processor cores (despite another four times speedup), here is a high quality animation loop.